Álgebra sobre un cuerpo

En matemáticas, un álgebra sobre un cuerpo K, o una K -álgebra, es un espacio vectorial A sobre K equipado con una noción compatible de multiplicación de elementos de A. Una generalización directa admite que K sea cualquier anillo conmutativo. Algunos autores utilizan el término "álgebra" como sinónimo de "álgebra asociativa".

Definiciones

Para ser exactos, sea $(V_mathbb{K},+)$ un espacio vectorial sobre el cuerpo $mathbb{K}$ , y supongamos que existe una operación binaria definida entre vectores:

$(cdot,cdot):V_mathbb{K}times V_mathbb{K} to V_mathbb{K}$

Tal que es bilineal y distributiva respecto a la suma, es decir, tal que para todo $u,v,w in V, lambda in mathbb{K}$ :

$ucdot(v+w) = ucdot v + ucdot w$
$(v+w)cdot u = vcdot u + wcdot u$
$ucdot(lambda v) = (lambda u)cdot v = lambda (ucdot v)$

Entonces con esta operación, 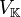$V_mathbb{K}$ se convierte en un álgebra sobre $mathbb{K}$ y $mathbb{K}$ es el cuerpo base del álgebra $mathcal{A}=(V_mathbb{K},+,cdot)$ . La segunda operación se llama "multiplicación". Sin embargo, la operación en varias clases especiales de álgebra toma diversos nombres:

Las álgebras también se pueden definir más generalmente sobre cualquier anillo unitario $R$ : necesitamos un módulo $mathcal{A}$ sobre $A$ y una operación bilineal de multiplicación que satisfaga las mismas identidades que arriba; entonces $mathcal{A}$ es una $R$ -álgebra, y $R$ es el anillo bajo $mathcal{A}$ . Dos álgebras $mathcal{A}$ y $mathcal{B}$ sobre $mathbb{K}$ son isomorfas si existe una K biyección - función lineal f: $mathcal{A} to mathcal{B}$ tal que f (xy) = f(x)f(y) para todo x, y en $mathcal{A}$ . Para todos los propósitos prácticos, las álgebras isomorfas son idénticas; solamente se diferencian en la notación de sus elementos.

Características

Para las álgebras sobre un cuerpo, la multiplicación bilineal de $mathcal{A} times mathcal{A}$ a $mathcal{A}$ es determinada totalmente por la multiplicación de los elementos de la base de A. Inversamente, una vez que ha sido elegida una base para $mathcal{A}$ , los productos de los elementos de base se pueden fijar arbitrariamente, y entonces extender de una manera única a un operador bilineal en $mathcal{A}$ , es decir de modo que la multiplicación que resulta satisfaga las leyes del álgebra.

Así, dado el cuerpo K, cualquier álgebra se puede especificar salvo un isomorfismo dando su dimensión (digamos n), y especificar los n³ coeficientes de estructura c_i,j,k, que son escalares. Estos coeficientes de estructura determinan la multiplicación en $mathcal{A}$ vía la regla siguiente:

$mathbf{e}_{i} mathbf{e}_{j} = sum_{k=1}^n c_{i,j,k} mathbf{e}_{k}$

Donde e₁,...e_n una base de A. El único requisito en los coeficientes de la estructura es que, si la dimensión n es un número infinito, entonces esta suma debe converger (en cualquier sentido que sea apropiado para la situación). Observe, sin embargo, que diversos conjuntos de coeficientes de estructura pueden dar lugar a álgebras isomorfas.

En física matemática, los coeficientes de estructura se escriben a menudo c_i,j^k, y se escribe usando el convenio de sumación de Einstein como

e_i e_j = c _i,j^k e_k.

Si se aplica esto a vectores escritos en notación de índice, entonces se convierte en

(xy)^k = c _i,j ^k xⁱ y^j.

Si K es solamente un anillo conmutativo y no un cuerpo, entonces lo mismo funciona si $mathcal{A}$ es un módulo libre sobre K. Si no es, entonces la multiplicación todavía está determinada totalmente por su acción en un conjunto generador de $mathcal{A}$ ; sin embargo, las constantes de estructura no se pueden especificar arbitrariamente en este caso, y saber solamente las constantes de estructura no específica el álgebra módulo isomorfismo.

Clases de álgebra y ejemplos

Un álgebra conmutativa es una en que la multiplicación es conmutativa; un álgebra asociativa es una en que la multiplicación es asociativa. Éstas incluyen las clases más familiares de álgebra.

Álgebras asociativas

Entre los ejemplos de álgebra asociativa podemos destacar:

- el álgebra de todas las matrices n-por-n sobre el cuerpo (o anillo conmutativo) K. Aquí la multiplicación es multiplicación ordinaria de matrices.
- las álgebra grupo, donde un grupo sirve de base del espacio vectorial y la multiplicación del álgebra amplía la multiplicación del grupo.
- el álgebra conmutativa K[x] de todos los polinomios sobre K, es un espacio vectorial de dimensión infinita (alef-0) sobre el cuerpo en el que se definen.
- las álgebras de funciones, tales como el R-álgebra de todas las funciones continuas real-valoradas definidas en el intervalo [0, 1], o la C-álgebra de todas las funciones holomórficas definidas en algún conjunto abierto en el plano complejo. Éstas son también conmutativos.
- las álgebras de incidencia se construyen sobre ciertos conjuntos parcialmente ordenados.
- las álgebras de operadores lineales, por ejemplo en un espacio de Hilbert. Aquí la multiplicación del álgebra viene dada por la composición de operadores. Estas álgebras también llevan una topología; se definen muchas de ellas en un espacio subyacente de Banach que las convierte en un álgebra de Banach. Si una involución se da también, obtenemos B-estrella-álgebras y C-estrella-álgebras. Éstas se estudian en análisis funcional.

Álgebras no asociativas

Las clases más conocidas de álgebras no-asociativas son las que son casi asociativas, es decir, en que una cierta ecuación simple obliga las diferencias entre diversas maneras de asociar la multiplicación de elementos. Éstos incluyen:

Álgebra de Lie, para las cuales requerimos la identidad de Jacobi z ( xy ) + (yz) x + (zx) y = 0 y anticonmutatividad: xx = 0. Para estas álgebra el producto se llama el corchete de Lie y se escribe [ x,y ] en vez de xy. Los ejemplos incluyen:
- Espacio euclidiano R³ con la multiplicación dada por el producto vectorial (con K el cuerpo R de los números reales);
- Álgebra de los campos vectoriales en una variedad diferenciable (si K es R o los números complejos C) o una variedad algebraica (para el general K);
- Cada álgebra asociativa da lugar a un álgebra de Lie usando el conmutador como corchete de Lie. De hecho cada álgebra de Lie se puede construir de esta manera, o es una subálgebra de un álgebra de Lie así construida.

Álgebra de Jordan, para las cuales requerimos (xy)x² = x(yx²) y también xy = yx.
- Cada álgebra asociativa sobre un cuerpo de característica distinta de 2 da lugar a un álgebra de Jordan definiendo una nueva multiplicación x*y = (1/2)(xy + yx). En contraste con el caso del álgebra de Lie, no toda álgebra de Jordan se puede construir de esta manera. Las que si se pueden se llaman especiales.

Álgebras alternativas, para las cuales requerimos que (xx)y =x(xy) y (yx)x = y(xx). Los ejemplos más importantes son los octoniones (un álgebra sobre los reales), y generalizaciones de los octoniones sobre otros cuerpos. (todas las álgebras asociativas son obviamente alternativas.) Salvo isomorfismo las únicas álgebras alternativas reales finito-dimensionales son los reales, los complejos, los cuaterniones y los octoniones.

Álgebras potencia-asociativas, para las cuales requerimos que x^mxⁿ = x^m+n, donde m ≥ 1 y n ≥ 1. (aquí definimos formalmente xⁿ⁺¹ recurrentemente como x (x ⁿ).) Los ejemplos incluyen todas las álgebras asociativas, todas las álgebras alternativas, y los sedeniones.